---

Electrical Quantity Division Principles

---

---

---

Electrical Quantity Division Principles

---

 

In this chapter, let us discuss about the following two division principles of electrical quantities.

• Current Division Principle
• Voltage Division Principle

Current Division Principle

When two or more passive elements are connected in parallel, the amount of current that flows through each element gets divided (shared) among themselves from the current that is entering the node.

Consider the following circuit diagram.

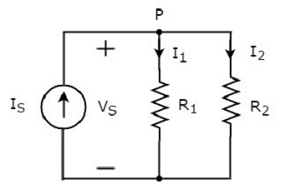
The above circuit diagram consists of an input current source I_S in parallel with two resistors R₁ and R₂. The voltage across each element is V_S. The currents flowing through the resistors R₁ and R₂ are I₁ and I₂ respectively.

The KCL equation at node P will be

 

IS=I1+I2??=?1+?2

• Substitute I1=VSR1?1=???1 and I2=VSR2?2=???2 in the above equation.

 

IS=VSR1+VSR2=VS?R2+R1R1R2???=???1+???2=????2+?1?1?2?

 

⇒VS=IS?R1R2R1+R2?⇒??=????1?2?1+?2?

• Substitute the value of V_S in I1=VSR1?1=???1.

 

I1=ISR1?R1R2R1+R2??1=???1??1?2?1+?2?

 

⇒I1=IS?R2R1+R2?⇒?1=????2?1+?2?

• Substitute the value of V_S in I2=VSR2?2=???2.

 

I2=ISR2?R1R2R1+R2??2=???2??1?2?1+?2?

 

⇒I2=IS?R1R1+R2?⇒?2=????1?1+?2?

From equations of I₁ and I₂, we can generalize that the current flowing through any passive element can be found by using the following formula.

 

IN=IS?Z1?Z2?...?ZN−1Z1+Z2+...+ZN???=????1??2?...???−1?1+?2+...+???

This is known as current division principle and it is applicable, when two or more passive elements are connected in parallel and only one current enters the node.

Where,

• I_N is the current flowing through the passive element of N^th branch.

• I_S is the input current, which enters the node.

• Z₁, Z₂, …,Z_N are the impedances of 1^st branch, 2^nd branch, …, N^th branch respectively.

Voltage Division Principle

When two or more passive elements are connected in series, the amount of voltage present across each element gets divided (shared) among themselves from the voltage that is available across that entire combination.

Consider the following circuit diagram.

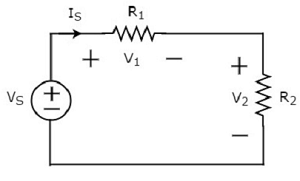
The above circuit diagram consists of a voltage source, V_S in series with two resistors R₁ and R₂. The current flowing through these elements is I_S. The voltage drops across the resistors R₁ and R₂ are V₁ and V₂ respectively.

The KVL equation around the loop will be

 

VS=V1+V2??=?1+?2

• Substitute V₁ = I_S R₁ and V₂ = I_S R₂ in the above equation

 

VS=ISR1+ISR2=IS(R1+R2)??=???1+???2=??(?1+?2)

 

IS=VSR1+R2??=???1+?2

• Substitute the value of I_S in V₁ = I_S R₁.

 

V1=?VSR1+R2?R1?1=????1+?2??1

 

⇒V1=VS?R1R1+R2?⇒?1=????1?1+?2?

• Substitute the value of I_S in V₂ = I_S R₂.

 

V2=?VSR1+R2?R2?2=????1+?2??2

 

⇒V2=VS?R2R1+R2?⇒?2=????2?1+?2?

From equations of V₁ and V₂, we can generalize that the voltage across any passive element can be found by using the following formula.

 

VN=VS?ZNZ1+Z2+....+ZN???=??????1+?2+....+???

This is known as voltage division principle and it is applicable, when two or more passive elements are connected in series and only one voltage available across the entire combination.

Where,

• V_N is the voltage across N^th passive element.

• V_S is the input voltage, which is present across the entire combination of series passive elements.

• Z₁,Z₂, …,Z₃ are the impedances of 1^st passive element, 2^nd passive element, …, N^th passive element respectively.

---

---

Frequently Asked Questions

---

---

---

---

---