Network Theory - Equivalent Circuits
Network Theory - Equivalent Circuits
If a circuit consists of two or more similar passive elements and are connected in exclusively of series type or parallel type, then we can replace them with a single equivalent passive element. Hence, this circuit is called as an equivalent circuit.
In this chapter, let us discuss about the following two equivalent circuits.
- Series Equivalent Circuit
- Parallel Equivalent Circuit
Series Equivalent Circuit
If similar passive elements are connected in series, then the same current will flow through all these elements. But, the voltage gets divided across each element.
Consider the following circuit diagram.
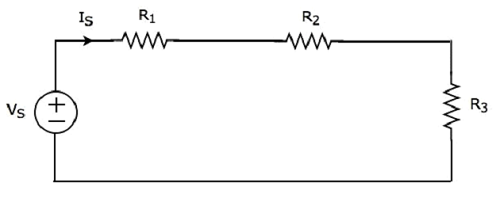
It has a single voltage source (VS) and three resistors having resistances of R1, R2 and R3. All these elements are connected in series. The current IS flows through all these elements.
The above circuit has only one mesh. The KVL equation around this mesh is
VS=V1+V2+V3??=?1+?2+?3
Substitute V1=ISR1,V2=ISR2?1=???1,?2=???2 and V3=ISR3?3=???3 in the above equation.
VS=ISR1+ISR2+ISR3??=???1+???2+???3
⇒VS=IS(R1+R2+R3)⇒??=??(?1+?2+?3)
The above equation is in the form of VS=ISREq??=????? where,
REq=R1+R2+R3???=?1+?2+?3
The equivalent circuit diagram of the given circuit is shown in the following figure.
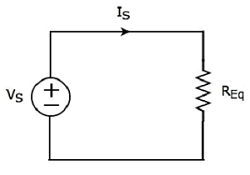
That means, if multiple resistors are connected in series, then we can replace them with an equivalent resistor. The resistance of this equivalent resistor is equal to sum of the resistances of all those multiple resistors.
Note 1 − If ‘N’ inductors having inductances of L1, L2, ..., LN are connected in series, then the equivalent inductance will be
LEq=L1+L2+...+LN???=?1+?2+...+??
Note 2 − If ‘N’ capacitors having capacitances of C1, C2, ..., CN are connected in series, then the equivalent capacitance will be
1CEq=1C1+1C2+...+1CN1???=1?1+1?2+...+1??
Parallel Equivalent Circuit
If similar passive elements are connected in parallel, then the same voltage will be maintained across each element. But, the current flowing through each element gets divided.
Consider the following circuit diagram.
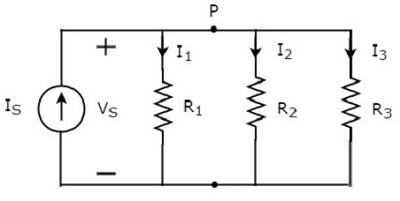
It has a single current source (IS) and three resistors having resistances of R1, R2, and R3. All these elements are connected in parallel. The voltage (VS) is available across all these elements.
The above circuit has only one principal node (P) except the Ground node. The KCL equation at this principal node (P) is
IS=I1+I2+I3??=?1+?2+?3
Substitute I1=VSR1,I2=VSR2?1=???1,?2=???2 and I3=VSR3?3=???3 in the above equation.
IS=VSR1+VSR2+VSR3??=???1+???2+???3
⇒IS=VS?1R1+1R2+1R3?⇒??=???1?1+1?2+1?3?
⇒VS=IS[1?1R1+1R2+1R3?]⇒??=??[1?1?1+1?2+1?3?]
The above equation is in the form of VS = ISREq where,
REq=1?1R1+1R2+1R3????=1?1?1+1?2+1?3?
1REq=1R1+1R2+1R31???=1?1+1?2+1?3
The equivalent circuit diagram of the given circuit is shown in the following figure.
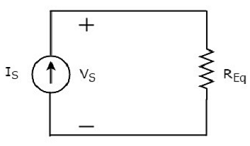
That means, if multiple resistors are connected in parallel, then we can replace them with an equivalent resistor. The resistance of this equivalent resistor is equal to the reciprocal of sum of reciprocal of each resistance of all those multiple resistors.
Note 1 − If ‘N’ inductors having inductances of L1, L2, ..., LN are connected in parallel, then the equivalent inductance will be
1LEq=1L1+1L2+...+1LN
Note 2 − If ‘N’ capacitors having capacitances of C1, C2, ..., CN are connected in parallel, then the equivalent capacitance will be
CEq=C1+C2+...+CN
