Network Theory - Delta to Star Conversion
Network Theory - Delta to Star Conversion
In the previous chapter, we discussed an example problem related equivalent resistance. There, we calculated the equivalent resistance between the terminals A & B of the given electrical network easily. Because, in every step, we got the combination of resistors that are connected in either series form or parallel form.
However, in some situations, it is difficult to simplify the network by following the previous approach. For example, the resistors connected in either delta (δ) form or star form. In such situations, we have to convert the network of one form to the other in order to simplify it further by using series combination or parallel combination. In this chapter, let us discuss about the Delta to Star Conversion.
Delta Network
Consider the following delta network as shown in the following figure.
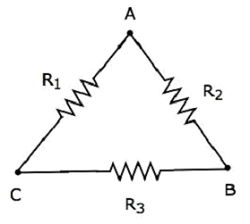
The following equations represent the equivalent resistance between two terminals of delta network, when the third terminal is kept open.
RAB=(R1+R3)R2R1+R2+R3???=(?1+?3)?2?1+?2+?3
RBC=(R1+R2)R3R1+R2+R3???=(?1+?2)?3?1+?2+?3
RCA=(R2+R3)R1R1+R2+R3
Star Network
The following figure shows the equivalent star network corresponding to the above delta network.
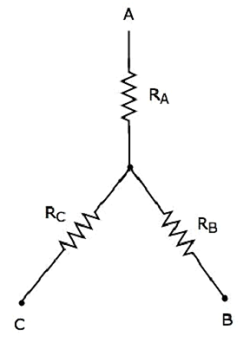
The following equations represent the equivalent resistance between two terminals of star network, when the third terminal is kept open.
RAB=RA+RB???=??+??
RBC=RB+RC???=??+??
RCA=RC+RA???=??+??
Star Network Resistances in terms of Delta Network Resistances
We will get the following equations by equating the right-hand side terms of the above equations for which the left-hand side terms are same.
RA+RB=(R1+R3)R2R1+R2+R3??+??=(?1+?3)?2?1+?2+?3 Equation 1
RB+RC=(R1+R2)R3R1+R2+R3??+??=(?1+?2)?3?1+?2+?3 Equation 2
RC+RA=(R2+R3)R1R1+R2+R3??+??=(?2+?3)?1?1+?2+?3 Equation 3
By adding the above three equations, we will get
2(RA+RB+RC)=2(R1R2+R2R3+R3R1)R1+R2+R32(??+??+??)=2(?1?2+?2?3+?3?1)?1+?2+?3
⇒RA+RB+RC=R1R2+R2R3+R3R1R1+R2+R3⇒??+??+??=?1?2+?2?3+?3?1?1+?2+?3 Equation 4
Subtract Equation 2 from Equation 4.
RA+RB+RC−(RB+RC)=R1R2+R2R3+R3R1R1+R2+R3−(R1+R2)R3R1+R2+R3??+??+??−(??+??)=?1?2+?2?3+?3?1?1+?2+?3−(?1+?2)?3?1+?2+?3
RA=R1R2R1+R2+R3??=?1?2?1+?2+?3
By subtracting Equation 3 from Equation 4, we will get
RB=R2R3R1+R2+R3??=?2?3?1+?2+?3
By subtracting Equation 1 from Equation 4, we will get
RC=R3R1R1+R2+R3??=?3?1?1+?2+?3
By using the above relations, we can find the resistances of star network from the resistances of delta network. In this way, we can convert a delta network into a star network.
Example
Let us calculate the resistances of star network, which are equivalent to that of delta network as shown in the following figure.
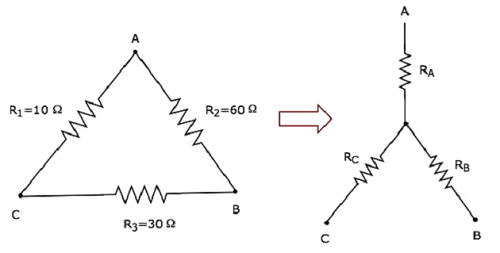
Given the resistances of delta network as R1 = 10 Ω, R2 = 60 Ω and R3 = 30 Ω.
We know the following relations of the resistances of star network in terms of resistances of delta network.
RA=R1R2R1+R2+R3??=?1?2?1+?2+?3
RB=R2R3R1+R2+R3??=?2?3?1+?2+?3
RC=R3R1R1+R2+R3??=?3?1?1+?2+?3
Substitute the values of R1, R2 and R3 in the above equations.
RA=10×6010+60+30=600100=6Ω??=10×6010+60+30=600100=6Ω
RB=60×3010+60+30=1800100=18Ω??=60×3010+60+30=1800100=18Ω
RC=30×1010+60+30=300100=3Ω??=30×1010+60+30=300100=3Ω
So, we got the resistances of star network as RA = 6 Ω, RB = 18 Ω and RC = 3 Ω, which are equivalent to the resistances of the given delta network.
